Come abitante di Arezzo, amante del medioevo, appassionato giocatore e professore di matematica e fisica, la Giostra del Saracino esercita da sempre su di me un fascino atavico: come gestore del progetto online Eduplay – Prof Marrelli, che si occupa di cultura nei giochi, non ho potuto sottrarmi da un’analisi di quelle che sono le grandezze fisiche e matematiche in gioco della Giostra.
Cominciamo ad analizzare i vari elementi che agiscono sulla carriera: il primo è indubbiamente la lunghezza della lizza, la pedana di terra che attraversa Piazza Grande in diagonale e che misura 46 metri.
Due fotocellule misurano i tempi di percorrenza della carriera: per essere valida, da regolamento tecnico, la lizza dev’essere percorsa in massimo 4,85 secondi, mentre la durata media si aggira attorno ai 4,6 secondi.
Se andiamo a calcolare la velocità media, cioè il rapporto tra lo spazio percorso e il tempo impiegato (Spazio/Tempo) vediamo che si tratta di circa 10 metri al secondo, pari a 36 km/h.
Se però immaginiamo che il cavallo inizi fermo e acceleri in maniera costante, otteniamo una velocità all’impatto pari al doppio: oltre i 70km/h.
Si tratta tuttavia di velocità ai limiti di quelle tipiche del galoppo del cavallo, dunque probabilmente la velocità effettiva di impatto è da qualche parte a metà tra questi due possibili valori.
Durante la cavalcata, il nostro fantino prende la mira sulla targa del buratto, lo scudo sul quale è posto il tabellone numerico.
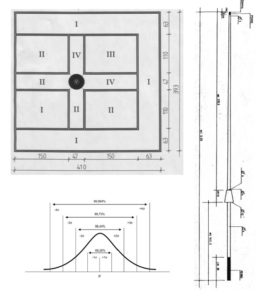
Se calcoliamo l’area delle varie zone, partendo dallo schema contenuto sul regolamento tecnico, vediamo che le aree che valgono un punto prendono una superficie pari a circa il 53% del totale: si scende poi a circa il 28% per il due, 10% per il tre, 8% per il quattro e poco più dell’1% per l’agognato cinque.
Tuttavia, la quantità di carriere ottime con punteggi di 4 e 5, soprattutto negli ultimi anni, è incrementata notevolmente: questo perché, ovviamente, i cavalieri si allenano duramente per mirare durante il galoppo.
Il colpo di lancia è indirizzato verso un punto e ha una certa probabilità di colpire un’area attorno ad esso: la funzione che descrive questo andamento è la Curva di Gauss.
La curva fornisce la probabilità di una certa quantità rispetto al suo valore medio: per esempio, se prendiamo l’altezza delle persone, molte di esse avranno un’altezza vicina all’altezza media mentre poche saranno molto alte o molto basse.
Uno dei parametri di questa funzione matematica è la “Sigma”, detta deviazione standard, che ci dice quanto è “spanciata” la curva: una “Sigma” molto piccola implicherà pochi casi lontani dalla media, mentre una molto grande implicherà la possibilità di allontanarsi da essa significativamente e relativamente spesso.
Immaginando di applicare la curva alla posizione del colpo sulla targa, che il nostro cavaliere sia molto capace miri al 5, possiamo immaginare che questo parametro sia di 10 cm.
Il colpo avrà allora una probabilità del 68% di cadere in un cerchio di raggio 10 cm attorno al punto mirato: facendo un po’ di conti, la probabilità di prendere 5 sarebbe quasi del 16%.
Chiaramente questo processo, apparentemente lineare, è ulteriormente complicato dalla presenza della lancia: la distanza tra la sua punta e il cavaliere è attorno ai due metri e mezzo.
La targa stessa è grande circa 40 cm: questo significa che, puntando al centro, il cavaliere ha a disposizione solo un totale di 9 gradi di angolo, in orizzontale e in verticale, per colpire la targa, riducendosi ad appena un grado entro il quale è in grado di prendere in cinque!
Inoltre, la lancia può cadere annullando completamente il punteggio di quella carriera.
Se però la lancia dovesse rompersi, il punteggio raddoppierà: questo potrebbe portare il cavaliere a tentare di giocare di forza, lanciando il cavallo alla velocità massima possibile e spingendo sulla lancia con tutto il peso.
Tuttavia, sulle prime 130 giostre da almeno 8 carriere, la lancia si è rotta solo 26 volte, meno del 2% delle carriere. Inoltre, ad oggi, i quartieri con più lance rotte sono quelli con meno vittorie e viceversa: insomma, la fortuna è davvero cieca e potrebbe non essere il caso farci troppo affidamento!
da “L’Alfiere” – n. III – 2019, pagg. 10-11
